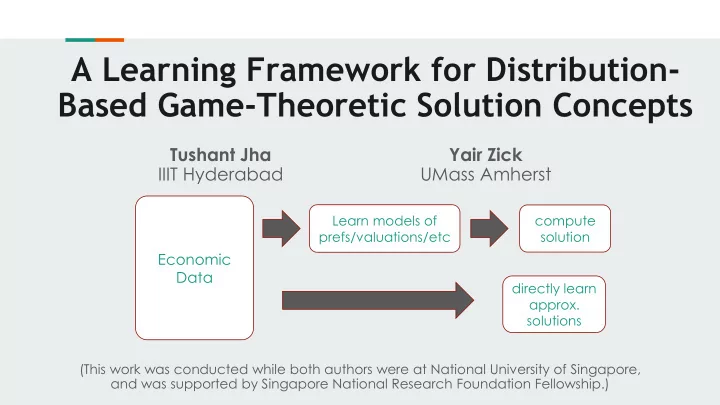
A Learning Framework for Distribution- Based Game-Theoretic Solution - PowerPoint PPT Presentation

A Learning Framework for Distribution- Based Game-Theoretic Solution Concepts Tushant Jha Yair Zick IIIT Hyderabad UMass Amherst Learn models of compute prefs/valuations/etc solution Economic Data directly learn approx. solutions (This work was conducted while both authors were at National University of Singapore, and was supported by Singapore National Research Foundation Fellowship.)

General Model of PAC Solution Concepts Observations from 𝒠 over game space 𝒴 probability ≥ 1 − δ , over training samples The probability that we observe a loss is low Find solution 𝑡 ∗ ∈ 𝕋 𝑌∼𝒠 𝜇 𝑕, 𝑌, 𝑡 ∗ Pr < 𝜁 Evaluated by an • Dimension theory for economic unknown game solution concepts 𝑕: 𝒴 → 𝒵 • Sample complexity bounds • Are consistent algorithms enough?

Example: PAC Solutions for Markets Observations, of item bundles and the utilities of n players for them, sampled i.i.d. from 𝒠 A sampled set of goods 𝑤 1 𝑡 1 , 𝑤 2 𝑡 1 … 𝑤 𝑜 (𝑡 1 ) Find an 𝑇 ⊆ 𝐻 is not demanded allocation by any player 𝑗 ∈ 𝑂 and prices 𝑤 1 𝑡 2 , 𝑤 2 𝑡 2 … 𝑤 𝑜 (𝑡 2 ) 〈𝐵 ∗ , Ԧ 𝑞 ∗ 〉 𝑇∼𝒠 Demands i 𝑇; 𝐵 ∗ , Ԧ 𝑞 ∗ Pr < 𝜁 𝑤 1 𝑡 3 , 𝑤 2 𝑡 3 … 𝑤 𝑜 (𝑡 3 ) • We prove linear solution dimension. • Therefore, prove polynomial sample complexity Evaluated by bound for PAC solvability. ⋮ • Also, we show existence of PAC solutions for unknown player Fisher markets (ie. budget constrained) and preferences 𝑤 𝑗 𝑗∈𝑂 markets with endowments.

Main Takeaway Recovers previous results such as: Enables i) PAC Core Stability in TU generalization of Cooperative Games approach to other (Balcan et al. IJCAI 2015), ii) in Hedonic Games domains like Markets, (Sliwinski et al. IJCAI 2017; Voting, Auctions, etc. Igarashi et al. AAAI 2019), iii) And others… Provides a unified formal approach for proving learnability in economics, and associated distribution-agnostic sample complexity bounds.