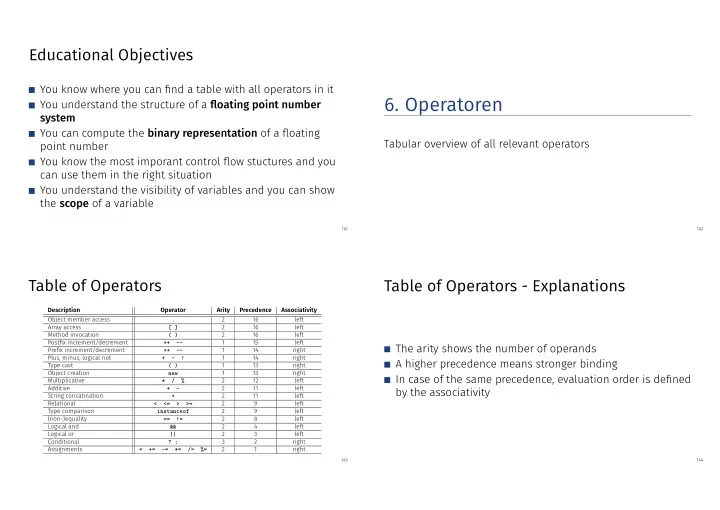

Educational Objectives You know where you can find a table with all operators in it 6. Operatoren You understand the structure of a floating point number system You can compute the binary representation of a floating Tabular overview of all relevant operators point number You know the most imporant control flow stuctures and you can use them in the right situation You understand the visibility of variables and you can show the scope of a variable 141 142 Table of Operators Table of Operators - Explanations Description Operator Arity Precedence Associativity Object member access 2 16 left . Array access 2 16 left [ ] Method invocation 2 16 left ( ) Postfix increment/decrement 1 15 left ++ -- The arity shows the number of operands Prefix increment/decrement 1 14 right ++ -- Plus, minus, logical not 1 14 right + - ! A higher precedence means stronger binding Type cast 1 13 right ( ) Object creation 1 13 right new In case of the same precedence, evaluation order is defined Multiplicative 2 12 left * / % Additive 2 11 left by the associativity + - String concatination 2 11 left + Relational 2 9 left < <= > >= Type comparison 2 9 left instanceof (non-)equality 2 8 left == != Logical and 2 4 left && Logical or 2 3 left || Conditional 3 2 right ? : Assignments 2 1 right = += -= *= /= %= 143 144
We remember from last time What is going on here? public class Main { public static void main(String[] args) { 7. Floating Point Numbers input 1.1 Out.print("First number =? "); float n1 = In.readFloat(); input 1.0 Out.print("Second number =? "); Floating Point Number Systems; IEEE Standard; float n2 = In.readFloat(); input 0.1 Out.print("Their difference =? "); float d = In.readFloat(); Out.print("computed difference - input difference = "); Out.println(n1-n2-d); output 2.2351742E-8 } } 145 146 Why is this happening? Floating Point Number Representation represented with Basis β : ± d 0 • d 1 . . . d p − 1 × β e , Not all real numbers can be represented Example β = 10 Representations of the decimal number 0.24 Rounding errors can propagate and amplify throughout program execution or or or 2 . 4 · 10 − 1 0 . 24 · 10 0 0 . 042 · 10 1 . . . ⇒ We want to understand why this is happening! = Example β = 2 Representations of the binary number 0.11 or or or 1 . 1 · 2 − 1 0 . 11 · 2 0 0 . 011 · 2 1 . . . 147 148
Caution: Holes in Value Range! Binary and Decimal Systems Example: β = 2 , 2 decimal places, only positive numbers Internally the computer computes with β = 2 d 0 • d 1 d 2 e = − 2 e = − 1 e = 0 e = 1 e = 2 ( binary system ) 1 . 00 2 0 . 25 0 . 5 1 2 4 Literals and inputs have β = 10 1 . 01 2 0 . 3125 0 . 625 1 . 25 2 . 5 5 ( decimal system ) 1 . 10 2 0 . 375 0 . 75 1 . 5 3 6 ⇒ Inputs have to be converted! = 1 . 11 2 0 . 4375 0 . 875 1 . 75 3 . 5 7 0 8 149 150 1 . 11 · 2 2 = 7 1 . 00 · 2 − 2 = 1 4 Conversion Decimal → Binary Note Angenommen, 0 < x < 2 . Hence: x ′ = b − 1 • b − 2 b − 3 b − 4 . . . = 2 · ( x − b 0 ) Step 1 (for x ): Compute b 0 : The following content in the floating point numbers chapter 1 , if x ≥ 1 serves to better understand the topic, but won’t be checked b 0 = 0 , otherwise in the exam. Step 2 (for x ): Compute b − 1 , b − 2 , . . . : Go to step 1 (for x ′ = 2 · ( x − b 0 ) ) 151 153
Binary Number Representations of 1 . 1 and Binary representation of 1 . 1 0 . 1 x b i x − b i 2( x − b i ) are not finite, there are errors when converting into a 1 . 1 b 0 = 1 0 . 1 0 . 2 (finite) binary floating point system. 0 . 2 b − 1 = 0 0 . 2 0 . 4 1.1f and 0.1f do not equal 1 . 1 and 0 . 1 , but slightly 0 . 4 b − 2 = 0 0 . 4 0 . 8 inaccurate approximation of these numbers. 0 . 8 b − 3 = 0 0 . 8 1 . 6 1 . 6 b − 4 = 1 0 . 6 1 . 2 = 1 . 1000000000000000888178 . . . 1.1 1 . 2 b − 5 = 1 0 . 2 0 . 4 = 1 . 1000000238418 . . . 1.1f ⇒ 1 . 00011 , periodic, not finite 154 155 Computing with Floating Point Numbers The IEEE Standard 754 for float Example β = 2 , p = 4 (4 digits precision): 1 sign bit 1 . 111 · 2 − 2 23 bit for the mantissa (leading bit is 1 and is not stored) 1 . 011 · 2 − 1 + 8 bit for the exponent (256 possible values)(254 possible exponents, 2 special values: 0 , ∞ ,...) ⇒ 32 bit overal. = 1 . 001 · 2 0 1. adjust exponents by denormalizing of one number 2. binary addition of the mantissa 3. renormalize 4. round to p significant places, if necessary 156 157
32-bit Representation of a Floating Point The IEEE Standard 754 for double Number 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 1 sign bit Exponent Mantisse 52 bit for the mantissa (leading bit is 1 and is not stored) ± 11 bit for the exponent (2046 possible exponents, 2 special values: 0 , ∞ ,...) ⇒ 64 bit overal. 2 − 126 , . . . , 2 127 1 . 00000000000000000000000 . . . ± 0 , ∞ , . . . 1 . 11111111111111111111111 158 159 Statements 8. Control Structures A statement is ... comparable with a sentence in natural language a complete execution unit Selection Statements, Iteration Statements, Termination, always finished with a semicolon Blocks, Visibility, Local Variables, Switch Statement f = 9f * celsius / 5 + 32 ; 160 161
Statement types Blocks A block is ... Valid statements are: Declaration statement a group of statements allowed wherever statements are allowed Assignments float aValue; aValue = 8933.234; Represented by curly braces Increment/decrement aValue++; expressions { Out.println(aValue); statement1 Method calls new Student(); statement2 . . Object-creation expressions ; . } Null statement 162 163 Control Flow Selection Statements up to now linear (from top to bottom) For interesting programs we need “branches” and “jumps” implement branches Computation of 1 + 2 + ... + n . if statement ja Eingabe n s := s + i; if-else statement i ≤ n ? i := 1; s := 0 i := i+ 1 nein Ausgabe s 164 165
if -Statement if-else -statement If condition is true then if ( condition ) if ( condition ) If condition is true then statement1 is executed, oth- statement1 statement statement is executed erwise statement2 is exe- else cuted. statement2 statement : arbitrary statement ( body of the condition : expression of int a = In.readInt(); int a = In.readInt(); if -Statement) type boolean if (a % 2 == 0){ if (a % 2 == 0) { condition : expression of statement1 : body of the Out.println("even"); Out.println("even"); type boolean if -branch } else { } Out.println("odd"); statement2 : body of the } else -branch 166 167 Layout! Iteration Statements implement “loops” int a = In.readInt(); if (a % 2 == 0){ for -statement Indentation Out.println("even"); while -statement } else { Indentation Out.println("odd"); do -statement } 168 169
for -Statement: Syntax Example: Compute 1 + 2 + ... + n // input Out.print("Compute the sum 1+...+n for n=?"); for ( init ; condition ; expression ) int n = In.readInt(); statement // computation of sum_{i=1}^n i int s = 0; init : expression statement, declaration statement, null for (int i = 1; i <= n; ++i){ statement s += i; condition : expression of type boolean } expression : any expression // output statement : any statement ( body of the for-statement) Out.println("1+...+" + n + " = " + s); 170 171 Example: Harmonic Numbers for -Statement: semantics The n -the harmonic number is for ( init ; condition ; expression ) statement 1 n H n = � i ≈ ln n. init is executed i =1 condition is evaluated true : Iteration starts This sum can be computed in forward or backward statement is executed direction, which mathematically is clearly equivalent expression is executed false: for -statement is ended. 172 173
Example: Harmonic Numbers Example: Harmonic Numbers Out.print("Compute H_n for n =? "); Results: int n = In.readInt(); float fs = 0; Compute H_n for n =? 10000000 for (int i = 1; i <= n; ++i){ Forward sum = 15.4037 fs += 1.0f / i; Backward sum = 16.686 } Out.println("Forward sum = " + fs); Compute H_n for n =? 100000000 float bs = 0; Forward sum = 15.4037 for (int i = n; i >= 1; --i){ bs += 1.0f / i; Backward sum = 18.8079 } Out.println("Backward sum = " + bs); 174 175 Example: Harmonic Numbers Example: Prime Number Test Observation: Def.: a natural number n ≥ 2 is a prime number, if no The forward sum stops growing at some point and is getting d ∈ { 2 , . . . , n − 1 } divides n . “really” wrong. The backward sum reasonably approximates H n . A loop that can test this: Explanation: int d; For 1 + 1 / 2 + 1 / 3 + · · · the late terms are too small to for (d=2; n%d != 0; ++d) { } actually contribute Floating Point Rule 2 176 177
Recommend
More recommend