1 t=1 t=2 t=1 t=2 $100 $100 $80 $80 $60 $60 $80 - PDF document

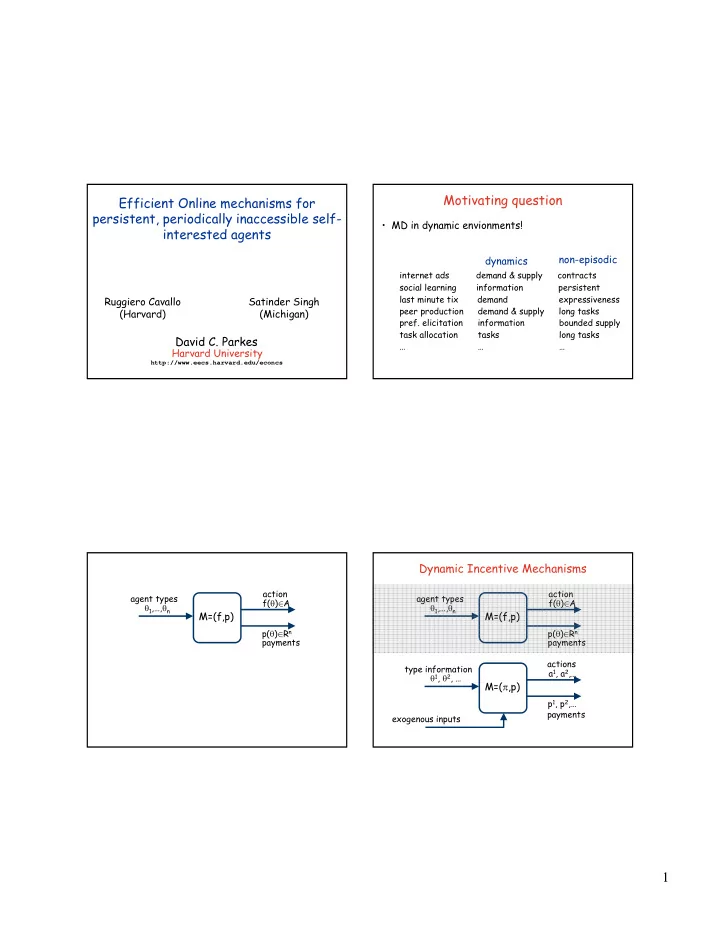
Motivating question Efficient Online mechanisms for persistent, periodically inaccessible self- • MD in dynamic envionments! interested agents non-episodic dynamics internet ads demand & supply contracts social learning information persistent Ruggiero Cavallo Satinder Singh last minute tix demand expressiveness peer production demand & supply long tasks (Harvard) (Michigan) pref. elicitation information bounded supply task allocation tasks long tasks David C. Parkes … … … Harvard University http://www.eecs.harvard.edu/econcs Dynamic Incentive Mechanisms action action agent types agent types f( θ ) ∈ A f( θ ) ∈ A θ 1 ,…, θ n θ 1 ,…, θ n M=(f,p) M=(f,p) p( θ ) ∈ R n p( θ ) ∈ R n payments payments actions type information a 1 , a 2 ,… θ 1 , θ 2 , … M=( π ,p) p 1 , p 2 ,… payments exogenous inputs 1

t=1 t=2 t=1 t=2 … … … … $100 $100 $80 $80 $60 $60 $80 One view from CS t=1 t=2 • Prior free: … • Typical setting: (e i ,d i ,v i ,q i ) • Body of work – Lavi & Nisan ’00 – Awerbuch et al. ’03 $100 … – Porter ’04 – Hajiaghayi, Kleinberg, Parkes’04 $80 – Blum & Hartline ’05 $60 – Hajiaghayi, Kleinberg, Mahdian, Parkes’05 – Lavi & Nisan ’05 $80 $60 – … • DSIC, monotonicity-based characterizations 2

One view from CS A second view • Prior free: • Center (and/or agents) have a probabilistic model of dynamics of environment π * (s) ∈ arg max a [r(s,a) + γ ∑ s’ ∈ St+1 Pr(s’,a,s)V * (s’)] • • Typical setting: (e i ,d i ,v i ,q i ) • Agents can misreport local model, local state • Body of work • Body of work: – Lavi & Nisan ’00 – Awerbuch et al. ’03 – Parkes & Singh ’03, ’04 – Porter ’04 – Cavallo, Parkes & Singh ’06 – Hajiaghayi, Kleinberg, Parkes’04 – Bergemann and Valamaki ’06 – Blum & Hartline ’05 – Cavallo, Parkes & Singh ’07 – Hajiaghayi, Kleinberg, Mahdian, Parkes’05 – … – Lavi & Nisan ’05 – … • typically interim IC, sometimes DSIC • DSIC, monotonicity-based characterizations. • Limited misreports: no-early arrival, no-late dep., etc. A second view type = static component (local model) • Center (and/or agents) have a probabilistic model of dynamics of environment π * (s) ∈ arg max a [r(s,a) + γ ∑ s’ ∈ St+1 Pr(s’,a,s)V * (s’)] • • Agents can misreport local model, local state • Body of work: – Parkes & Singh ’03, ’04 – Cavallo, Parkes & Singh ’06 – Bergemann and Valimaki ’06 – Cavallo, Parkes & Singh ’07 – Athey & Segal ’07 • typically interim IC, sometimes DSIC 3

type = static component (local model) type = static component (local model) + dynamic component (local state) + dynamic component (local state) type = static component (local model) type = static component (local model) + dynamic component (local state) + dynamic component (local state) 4

type = static component (local model) type = static component (local model) + dynamic component (local state) + dynamic component (local state) type = static component (local model) type = static component (local model) + dynamic component (local state) + dynamic component (local state) 5

policy π i : S i → A MDP: (S i ,A,r i , τ i ) V π i (s)=E[ ∑ k=t γ k-t r k i (s k i , π (s k ))] τ i (s i ,a) r i (s i ,a) V * i (s): π * i ∈ arg max π V π i (s) initial state s i 0 • Dynamic types, persistent agents • Dynamic types, arrival + departures • Dynamic types, accessible/inaccessible … policy π i : S i → A policy π i : S i → A MDP: (S i ,A,r i , τ i ) MDP: (S i ,A,r i , τ i ) V π i (s)=E[ ∑ k=t γ k-t r k i (s k i , π (s k ))] V π i (s)=E[ ∑ k=t γ k-t r k i (s k i , π (s k ))] τ i (s i ,a) r i (s i ,a) τ i (s i ,a) r i (s i ,a) V * i (s): π * i ∈ arg max π V π i (s) V * i (s): π * i ∈ arg max π V π i (s) initial state s i initial state s i 0 0 policy π : S → A policy π : S → A S=S 0 × S 1 × … × S n S=S 0 × S 1 × … × S n V π (s)=E[ ∑ k=t γ k-t r k (s k , π (s k ))] V π (s)=E[ ∑ k=t γ k-t r k (s k , π (s k ))] r(s,a)= ∑ i r i (s i ,a) r(s,a)= ∑ i r i (s i ,a) V * (s): π * ∈ arg max π V π (s) V * (s): π * ∈ arg max π V π (s) τ= ( τ 0 , τ 1 ,…, τ n ) τ 0 (s 0 ,a) τ= ( τ 0 , τ 1 ,…, τ n ) τ 0 (s 0 ,a) a ∈ A(s) a ∈ A(s) Assumption : CIA ( C onditional I ndependence given A ctions) r i ((s i ,s -i ),a)=r i ((s i ,s -i ’),a) … … τ i ((s i ,s -i ),a)= τ i ((s i ,s -i ’),a) 6

Example: Coordinated learning (CPS’06,BV’06) period t collect report states actions π * (s t ) payments report models … … … … strategy: history × type → report … … payment: V * (s -i ) – V * (s -i | π * (s) ) ⇒ interim IC (in every state) policy π : S → A S=S 0 × S 1 × … × S n V π (s)=E[ ∑ k=t γ k-t r k (s k , π (s k ))] period t r(s,a)= ∑ i r i (s i ,a) V * (s): π * ∈ arg max π V π (s) τ= ( τ 0 , τ 1 ,…, τ n ) a ∈ A(s) observe collect report states actions π * (s t ) actions payments report models make/suggest … A == {public|voluntary|private} private effects standard in MD OK if observable 7

arrival/departure process • Dynamic types, persistent agents • Dynamic types, arrival + departures • Dynamic types, accessible/inaccessible … arrival/departure process arrival/departure process … … 8

arrival/departure process arrival/departure process … … static type == (local model,initial state) arrival/departure process H(s 0 ): set of static types present s=(s 0 , {s i } i ∈ H(s0) ) ∈ S arrival process τ 0 : S 0 × A → S 0 r(s,a)= ∑ i ∈ H(s0) r i (s i ,a) departure: local absorbing state … … 9

static type == (local model,initial state) Special case: Deterministic Local Models H(s 0 ): set of static types present s=(s 0 , {s i } i ∈ H(s0) ) ∈ S • Only dynamics are arrival/departure of static types τ 0 : S 0 × A → S 0 arrival process • Agents arrive and declare reward for all future r(s,a)= ∑ i ∈ H(s0) r i (s i ,a) sequences of actions via deterministic local model departure: local absorbing state alloc alloc alloc alloc … 5 5 5 linear valuation 0 0 0 0 Assumption: CIA alloc alloc alloc alloc C onditional Independence given A ctions all-or-nothing Pr( θ t | θ 1..t-1 ,a 1..t-1 )=Pr( θ t |a 1..t-1 ) 0 0 0 100 … 0 0 0 0 0 alloc unit-demand 5 0 0 • Dynamic types, persistent agents • Dynamic types, arrival + departures • Dynamic types, accessible/inaccessible arrival/depature = inaccess → access → inaccess 10

• Augment local state with accessible/inaccessible • Augment local state with accessible/inaccessible • Inaccessible == no messages, no payments • Inaccessible == no messages, no payments • Can pretend to be inaccessible when not • Can pretend to be inaccessible when not accessible (but not vice versa) accessible (but not vice versa) • Actions can make an agent become inaccessible • Actions can make an agent become inaccessible • Can have reward for actions while inaccessible • Can have reward for actions while inaccessible • Assumption: run but can’t hide // pay the piper • Assumption: run but can’t hide // pay the piper Arr/dep & Static type A Belief-state MDP model Persistent & Dynamic type r(s i ,a) τ (s i ,a) CIA: r(s i ,a) τ (s i ,a) • P artially Observable M arkov D ecision P rocess Pr( θ t | θ 1..t −1 ,a 1..t-1 )=Pr( θ t |a 1..t-1 ) BV’06 • Model as a belief-state MDP (Kaelbling et al. 96) PS’03 V * -i (s)-V * -i (s| π * (s)) – BS=S 0 × BS 1 × … × BS n , BS i = ∆ (S i ) v i -(V * (s e )-V * (s e -i )) charge each period – when accessible, bs i ∈ BS i , reduces to point mass charge @ departure – r i (bs i t a): in expectation on underlying states – policy π * : BS → A Persistent, Access/inaccess, Arr/dep & Dynamic type dynamic type r(s i ,a) τ (s i ,a) r(s i ,a) τ (s i ,a) RBCH Pr( θ t | θ 1..t −1 ,a 1..t-1 )=Pr( θ t |a 1..t-1 ) CPS’07 CPS’07 charge V * -i (s)-V * -i (s| π * (s)) where δ t is # periods been charge each period inaccessible 11