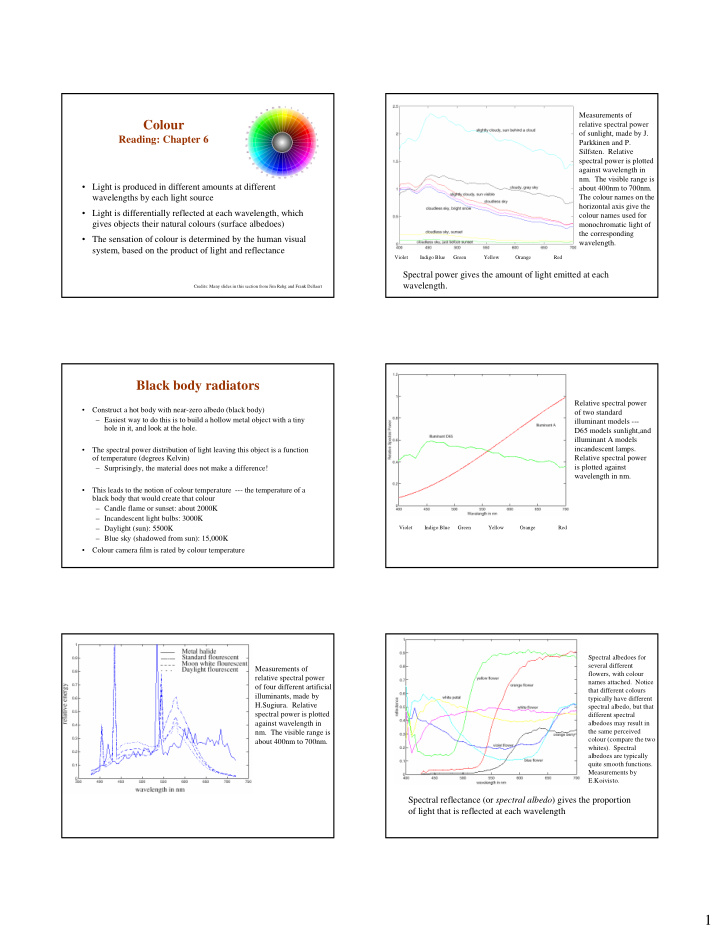



Measurements of Colour relative spectral power of sunlight, made by J. Reading: Chapter 6 Parkkinen and P. Silfsten. Relative spectral power is plotted against wavelength in nm. The visible range is • Light is produced in different amounts at different about 400nm to 700nm. wavelengths by each light source The colour names on the horizontal axis give the • Light is differentially reflected at each wavelength, which colour names used for gives objects their natural colours (surface albedoes) monochromatic light of the corresponding • The sensation of colour is determined by the human visual wavelength. system, based on the product of light and reflectance Violet Indigo Blue Green Yellow Orange Red Spectral power gives the amount of light emitted at each wavelength. Credits: Many slides in this section from Jim Rehg and Frank Dellaert Black body radiators Relative spectral power • Construct a hot body with near-zero albedo (black body) of two standard – Easiest way to do this is to build a hollow metal object with a tiny illuminant models --- hole in it, and look at the hole. D65 models sunlight,and illuminant A models incandescent lamps. • The spectral power distribution of light leaving this object is a function of temperature (degrees Kelvin) Relative spectral power is plotted against – Surprisingly, the material does not make a difference! wavelength in nm. • This leads to the notion of colour temperature --- the temperature of a black body that would create that colour – Candle flame or sunset: about 2000K – Incandescent light bulbs: 3000K – Daylight (sun): 5500K Violet Indigo Blue Green Yellow Orange Red – Blue sky (shadowed from sun): 15,000K • Colour camera film is rated by colour temperature Spectral albedoes for several different Measurements of flowers, with colour relative spectral power names attached. Notice of four different artificial that different colours illuminants, made by typically have different H.Sugiura. Relative spectral albedo, but that spectral power is plotted different spectral against wavelength in albedoes may result in the same perceived nm. The visible range is colour (compare the two about 400nm to 700nm. whites). Spectral albedoes are typically quite smooth functions. Measurements by E.Koivisto. Spectral reflectance (or spectral albedo ) gives the proportion of light that is reflected at each wavelength 1
The appearance of colours • Reflected light at each wavelength is the product of illumination and surface reflectance When one views a coloured surface, the • Surface reflectance is typically modeled as having two spectral radiance of components: the light reaching the eye depends on both – Lambertian reflectance: equal in all directions (diffuse) the spectral radiance – Specular reflectance: mirror reflectance (shiny spots) of the illuminant, and on the spectral albedo of the surface. colour Names for Cartoon Spectra Additive colour Mixing Subtractive colour Mixing Colour matching experiments - I • Show a split field to subjects; one side shows the light whose colour one wants to measure, the other a weighted mixture of primaries (fixed lights). 2
Colour Matching Process Colour Matching Experiment 1 ������������������������������������� ��������������������������� Colour Matching Experiment 1 Colour Matching Experiment 1 ��������������������������� ��������������������������� Colour Matching Experiment 2 Colour Matching Experiment 2 ��������������������������� ��������������������������� 3
Colour Matching Experiment 2 Colour matching experiments - II • Many colours can be represented as a positive weighted sum of A, B, C • write M=a A + b B + c C where the = sign should be read as “matches” • This is additive matching. • Gives a colour description system - two people who agree on A, B, C need only supply (a, b, c) to describe a colour. ��������������������������� Subtractive matching The principle of trichromacy • Some colours can’t be matched like this: • Experimental facts: instead, must write – Three primaries will work for most people if we allow subtractive matching M+a A = b B+c C • Exceptional people can match with two or only one • This is subtractive matching. primary (colour blindness) • Interpret this as (-a, b, c) • This could be caused by a variety of deficiencies. • Problem for building monitors: Choose R, G, B such that – Most people make the same matches. positive linear combinations match a large set of colours • There are some anomalous trichromats, who use three primaries but make different combinations to match. Human Photoreceptors Human Cone Sensitivities ����� ��������� • Spectral sensitivity of L, M, S (red, green, blue) cones in human eye 4
Grassman’s Laws Linear colour spaces RBG colour Matching • A choice of primaries • RGB: primaries are • monochromatic yields a linear colour monochromatic. Energies • 645.2, 526.3, 444.4 nm. space --- the coordinates are 645.2nm, 526.3nm, • negative parts -> some of a colour are given by 444.4nm. the weights of the colours can be matched • CIE XYZ: Primaries are primaries used to match it. only subtractively. imaginary, but have other • Choice of primaries is convenient properties. equivalent to choice of Colour coordinates are colour space. (X,Y,Z), where X is the amount of the X primary, etc. Figure courtesy of D. Forsyth CIE XYZ colour Matching Geometry of colour (CIE) • White is in the center, with saturation increasing towards the CIE XYZ: colour boundary matching functions are • Mixing two coloured lights positive everywhere, creates colours on a straight line but primaries are imaginary. • Mixing 3 colours creates colours within a triangle Usually draw x, y, • Curved edge means there are no where x=X/(X+Y+Z) 3 actual lights that can create all y=Y/(X+Y+Z) colours that humans perceive! So overall brightness is ignored. Figure courtesy of D. Forsyth 5
RGB colour Space The black-body locus (the colours of heated black-bodies). The colours that can be displayed on a typical computer monitor (phosphor limitations keep the space quite small) Figures courtesy of Uniform colour spaces ��������������� D. Forsyth • McAdam ellipses (next slide) demonstrate that differences in x,y are a poor guide to differences in colour – Each ellipse shows colours that are perceived to be the same • Construct colour spaces so that differences in coordinates are a good guide to differences in colour. 10 times actual size Actual size Non-linear colour spaces Adaptation phenomena • The response of your colour • Common example: walk inside • HSV: (Hue, Saturation, Value) are non-linear functions of system depends both on spatial from a bright day; everything XYZ. contrast and what it has seen looks dark for a bit, then takes – because hue relations are naturally expressed in a circle before (adaptation) its conventional brightness. • This seems to be a result of coding constraints -- receptors • Munsell: describes surfaces, rather than lights - less appear to have an operating relevant for graphics. Surfaces must be viewed under point that varies slowly over fixed comparison light time, and to signal some sort of offset. One form of adaptation involves changing this operating point. 6
Viewing coloured objects Finding Specularities • Assume we are dealing with dielectrics • Assume diffuse • Diffuse component (Lambertian) plus – specularly reflected light is the same colour as the – colour of reflected light specular model source depends on both illuminant and surface • Reflected light has two components • Specular component – diffuse – specularities on – specular dielectric (non- – and we see a weighted sum of these two metalic) objects take the colour of • Specularities produce a characteristic dogleg in the the light histogram of receptor responses – specularities on – in a patch of diffuse surface, we see a colour multiplied by different scaling constants (surface orientation) metals have colour of the metal – in the specular patch, a new colour is added; a “dog- leg” results 7
Recommend
More recommend