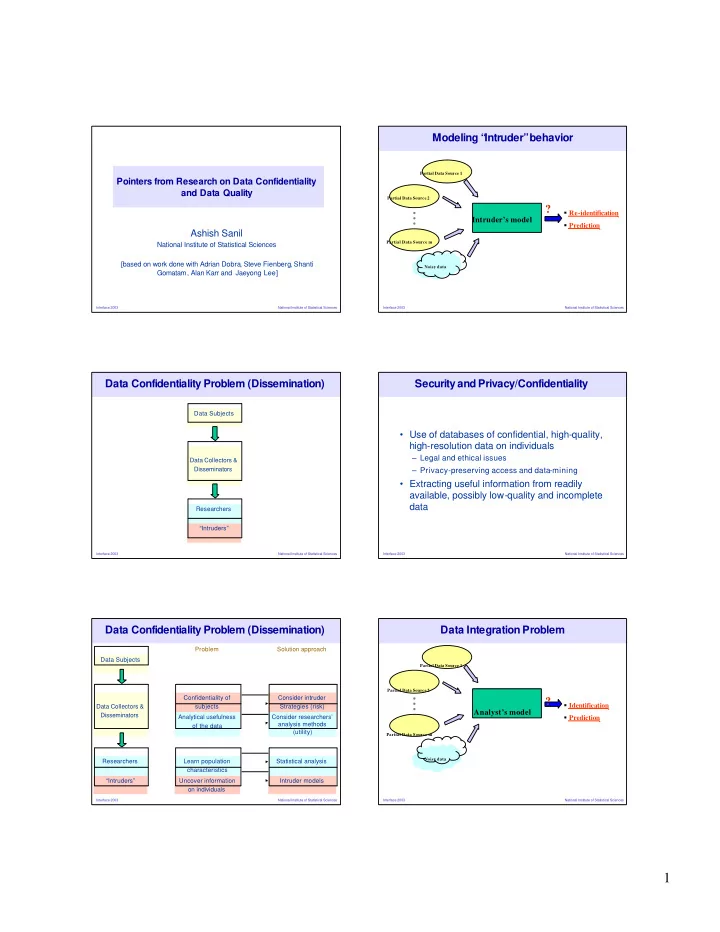

Modeling “ Intruder” behavior Partial Data Source 1 Pointers from Research on Data Confidentiality and Data Quality Partial Data Source 2 ? � Re-identification Intruder’s model � Prediction Ashish Sanil Partial Data Source m National Institute of Statistical Sciences [based on work done with Adrian Dobra, Steve Fienberg, Shanti Noisy data Gomatam, Alan Karr and Jaeyong Lee] Interface 2003 National Institute of Statistical Sciences Interface 2003 National Institute of Statistical Sciences Data Confidentiality Problem (Dissemination) Security and Privacy/Confidentiality Data Subjects • Use of databases of confidential, high-quality, high-resolution data on individuals – Legal and ethical issues Data Collectors & Disseminators – Privacy-preserving access and data-mining • Extracting useful information from readily available, possibly low-quality and incomplete data Researchers “Intruders” Interface 2003 National Institute of Statistical Sciences Interface 2003 National Institute of Statistical Sciences Data Confidentiality Problem (Dissemination) Data Integration Problem Problem Solution approach Data Subjects Partial Data Source 1 Partial Data Source 2 Confidentiality of Consider intruder ? � Identification Data Collectors & subjects Strategies (risk) Analyst’s model Disseminators � Prediction Analytical usefulness Consider researchers’ analysis methods of the data (utility) Partial Data Source m Noisy data Researchers Learn population Statistical analysis characteristics “Intruders” Uncover information Intruder models on individuals Interface 2003 National Institute of Statistical Sciences Interface 2003 National Institute of Statistical Sciences 1
Data Quality Issues Modeling Tools • Most probabilistic record linkage • DQ Problem : Evaluate data quality Noisy Data Partial Data based on Fellegi-Sunter model (consistency, accuracy, etc.) and try to — Match records in data files A and B • Rules-based • Techniques for improve it validity checks finding upper —Consider all pairs in A x B Determin. and lower —Estimate probability of observing • DC �� DQ Link : Like the intruder, we need bounds certain patterns (say, partial substring match) given true match, and given • Record linkage • Dis - to have a model/procedure to ascertain how non- match aggregation • Robust Inference methods —Decision rules for using the methods well we can do with the imperfect data • Reconstruction probabilities to declare record pairs as • Outlier detection techniques match, non-match or undecided • Implementation and scalability challenges • Large CS/Statistics literature Interface 2003 National Institute of Statistical Sciences Interface 2003 National Institute of Statistical Sciences Modeling Tools Modeling Tools Noisy Data Partial Data Noisy Data Partial Data • Rules-based • Techniques for • Rules-based validity • Techniques for finding validity checks finding upper checks upper and lower bounds Determin. and lower Deterministic • Outlier detection methods: bounds Statistical analogs of validity • Record linkage • Dis - • Record linkage • Dis-aggregation methods checks aggregation • Outlier Inference • Robust methods • Reconstruction techniques methods Inference detection • Need to determine if • Reconstruction • Robust • Outlier detection techniques sensitive relationships in the methods data can be learned by using robust statistical techniques Interface 2003 National Institute of Statistical Sciences Interface 2003 National Institute of Statistical Sciences Modeling Tools Modeling Tools • Verifying data types and ranges as defined in metadata Noisy Data Partial Data Noisy Data Partial Data • Reconstruction techniques • Check consistency • Rules-based • Techniques for • Rules-based • Techniques for finding upper validity checks finding upper validity checks (e.g., temporal constraints) such as Iterative Proportional Determin. Determin. and lower and lower • Parse and standardize Fitting (prediction from a log- bounds bounds (e.g., addresses) linear model) • Record linkage • Dis - • Record linkage • Dis - aggregation • Robust • Robust aggregation Inference Inference • Missing value imputation methods methods methods methods � Can detect anomalies/data • Reconstruction • Reconstruction methods • Outlier • Outlier techniques techniques detection detection distortion measures • Dis-aggregation strategies, � Part of Extract-Transform-Load e.g., simulating possible (ETL) process in data warehousing populations that satisfy the systems aggregation constraints � Often first step in record linkage Interface 2003 National Institute of Statistical Sciences Interface 2003 National Institute of Statistical Sciences 2
Example Scenario Example: Three Data Sources X Y Z D1 4 10 3 D2 2 14 29 Tracking shipments X Y Z • Vessels originating from two ports: O1, O2 O1 ?? O2 • Two ports of destination: D1, D2 O1 O2 • Carrying three kinds of cargo: X, Y, Z D1 D1 6 11 • Partial information available in the form of D2 28 17 D2 cross-tabulated numbers X Y Z O1 3 19 12 O2 3 5 20 Interface 2003 National Institute of Statistical Sciences Interface 2003 National Institute of Statistical Sciences Example: Three Data Sources Problem Formulation and Solution X Y Z D1 4 10 3 D2 2 14 29 • Denote the cell counts in the 3-way table by n i,j,k i={D1,D2}, j={O1,O2},k={X,Y,Z} • Objective: max/min n D1,O1,X O1 O2 • Subject to linear constraints on n i,j,k that D1 6 11 preserve the marginal totals; n i,j,k non- negative integers [E.g., n D1,O1,X + n D1,O2,X = 4] D2 28 17 • Use an Integer Programming solver to solve X Y Z • Result: 1 < n D1,O1,X < 1 O1 3 19 12 O2 3 5 20 Interface 2003 National Institute of Statistical Sciences Interface 2003 National Institute of Statistical Sciences Example: Three Data Sources Problem Solution (contd.) X Y Z D1 4 10 3 D2 2 14 29 • Example constructed to demonstrate the extreme case: All elements of the 3-way table are exactly determined from the 2-way marginals!! • More typically, we obtain sharp bounds on the cell O1 O2 counts How many of X from O1 � D1? D1 6 11 • Tightness of the bounds depends on: D2 28 17 – Dimension of marginals available – Number of marginals available X Y Z – Sparseness of the full table O1 3 19 12 O2 3 5 20 Interface 2003 National Institute of Statistical Sciences Interface 2003 National Institute of Statistical Sciences 3
Related Techniques “ Magnitude” tables • Simulation : Can run a Markov Chain Monte Carlo simulation to explore the space of all tables that Cells contain real-valued, additive quantities satisfy the marginal constraints (via Gröbner basis technology) • Linear Programming can be used for bounds • Iterative Proportional Fitting for table reconstruction • Cells with small count and/or dominant • Scalability : contributors are at higher risk of exposure – Heuristic Algorithms for bounds: “Shuttle Algorithm” –seems (Statistical Disclosure Control has the (n,p) - to work reasonably well when all (k-1) dimensional marginals rule which says, e.g., “Cells with n < 3 and are known for a k-dimensional table – Network Flow formulations for special cases where one of the three accounts for more – Linear Programming (ignore integrality constraints) than p=0.7 of the content should be – Decomposable Graphical Models considered risky”) Interface 2003 National Institute of Statistical Sciences Interface 2003 National Institute of Statistical Sciences Special Case: Decomposable Graphical Models Concluding Remarks • A large class of sets of available marginals can be represented as A undirected graphs (DC,DQ) methods can be useful • If the graph is decomposable • Need to explicitly modify them (triangulated) then explicit – Problem-specific knowledge B C formulas are available for the – Discard DC-specific characteristics bounds ( Fienberg-Dobra work) • Hopefully, added resources can also be used • [Graph on the right corresponds to the D E for tackling problems of scalability, etc. availability of the (A,B), (B,D,E),(B,C,E) marginal tables] Interface 2003 National Institute of Statistical Sciences Interface 2003 National Institute of Statistical Sciences References A • http://www.niss.org/dg : papers, references on cell-bounds and many other things B C • http://www.cs.cmu.edu/~wcohen/matching : Annotated bibliography on record linkage Leon Willenborg and Ton de Waal : • D E – “Statistical Disclosure Control in Practice” (1996), Springer Not decomposable! – “Elements of Statistical Disclosure Control” (2000), Springer Interface 2003 National Institute of Statistical Sciences Interface 2003 National Institute of Statistical Sciences 4
Recommend
More recommend