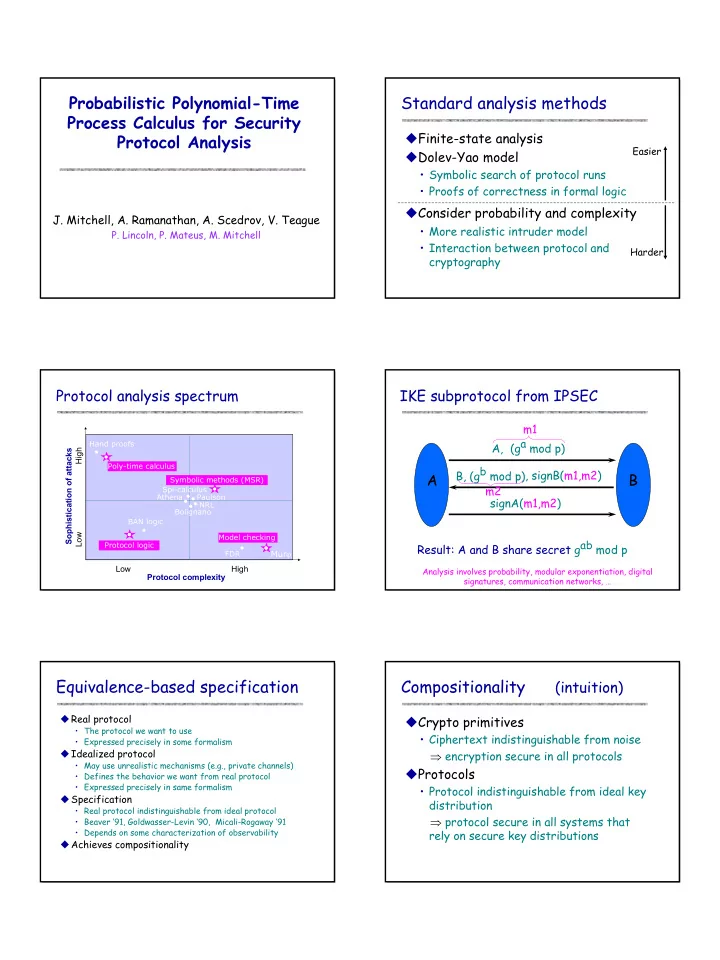

Probabilistic Polynomial-Time Standard analysis methods Process Calculus for Security � Finite-state analysis Protocol Analysis Easier � Dolev-Yao model • Symbolic search of protocol runs • Proofs of correctness in formal logic � Consider probability and complexity J. Mitchell, A. Ramanathan, A. Scedrov, V. Teague • More realistic intruder model P. Lincoln, P. Mateus, M. Mitchell • Interaction between protocol and Harder cryptography Protocol analysis spectrum IKE subprotocol from IPSEC m1 A, (g a mod p) Hand proofs Sophistication of attacks High � � Poly-time calculus B, (g b mod p) , signB(m1,m2) A B Symbolic methods (MSR) m2 Spi-calculus � Athena Paulson � signA(m1,m2) � � � NRL � Bolignano BAN logic � Low � � Model checking Result: A and B share secret g ab mod p Protocol logic � � � FDR Mur ϕ Low High Analysis involves probability, modular exponentiation, digital Protocol complexity signatures, communication networks, … Equivalence-based specification Compositionality (intuition) � Real protocol � Crypto primitives • The protocol we want to use • Ciphertext indistinguishable from noise • Expressed precisely in some formalism � Idealized protocol ⇒ encryption secure in all protocols • May use unrealistic mechanisms (e.g., private channels) � Protocols • Defines the behavior we want from real protocol • Expressed precisely in same formalism • Protocol indistinguishable from ideal key � Specification distribution • Real protocol indistinguishable from ideal protocol ⇒ protocol secure in all systems that • Beaver ‘91, Goldwasser-Levin ‘90, Micali-Rogaway ’91 • Depends on some characterization of observability rely on secure key distributions � Achieves compositionality 1
Roscoe ‘95, Schneider ‘96, Compositionality Language Approach Abadi-Gordon’97 � Intuitively, if: � Write protocol in process calculus • Q securely realizes I , • Dolev-Yao model • R securely realizes J, � Express security using observational equivalence • R, J use I as a component, • Standard relation from programming language theory � then P ≈ Q iff for all contexts C[ ], same R{Q/I} securely realizes J observations about C[P] and C[Q] � Fits well with process calculus • Inherently compositional • Context (environment) represents adversary because ≈ is a congruence � Use proof rules for ≈ to prove security • Q ≈ I ⇒ C[Q] ≈ C[I] • Protocol is secure if no adversary can distinguish it • contexts constructed from R, J, simulators from some idealized version of the protocol Great general idea; application is complicated A ≈ B C ≈ D Aspect of compositionality The proof is easy A|C ≈ B|D � Recall definition � Property of observational equiv P ≈ Q iff for all contexts C[ ], same observations about C[P] and C[Q] � Assume A ≈ B C ≈ D • A ≈ B ⇒ ∀ C[ ], C[A] ∼ C[B] A|C ≈ B|D � Therefore • For any C[ ], let C’[ • ] = C[ • | D] • By assumption, C’[A] ∼ C’[B] • Which means that A|D ≈ B|D similarly for other process forms � By similar reasoning • Can show A|C ≈ A|D • Therefore A|C ≈ A|D ≈ B|D Probabilistic Poly-time Analysis Pseudo-random number generators � Sequence generated from random seed � Add probability, complexity P n : let b = n k -bit sequence generated from n random bits � Probabilistic polynomial - t ime process calc in PUBLIC 〈 b 〉 end • Protocols use probabilistic primitives � Truly random sequence – Key generation, nonce, probabilistic encryption, ... Q n : let b = sequence of n k random bits • Adversary may be probabilistic in PUBLIC 〈 b 〉 end � Express protocol and spec in calculus � P is crypto strong pseudo - r andom number � Security using observational equivalence generator • Use probabilistic form of process equivalence P ≈ Q Equivalence is asymptotic in security parameter n 2
Secrecy for Challenge-Response Secrecy for Challenge-Response � Protocol P � Protocol P Non-malleability: A → B: { i } K A → B: { i } K Given only a ciphertext, it is difficult to generate B → A: { f(i) } K B → A: { f(i) } K a different ciphertext so that � “Obviously’’ secret protocol Q � “Obviously’’ secret protocol Q the respective plaintexts are related A → B: { random_number } K A → B: { random_number } K B → A: { random_number } K B → A: { random_number } K � Analysis: P ≈ Q reduces to crypto condition related to non-malleability [Dolev, Dwork, Naor] – Fails for “plain old” RSA if f(i) = 2i Security of encryption schemes Passive Adversary � Passive adversary • Semantic security m 0 , m 1 • Indistinguishability � Chosen ciphertext attacks (CCA1) E(m i ) Challenger Attacker • Adversary can ask for decryption before receiving a challenge ciphertext guess 0 or 1 � Chosen ciphertext attacks (CCA2) • Adversary can ask for decryption before and after receiving a challenge ciphertext Chosen ciphertext CCA1 Chosen ciphertext CCA2 c c D(c) D(c) m 0 , m 1 m 0 , m 1 Challenger Attacker E(m i ) E(m i ) Challenger Attacker guess 0 or 1 c ≠ E(m j ) D(c) guess 0 or 1 3
Specification with Authentication Research project � Define general system � Protocol P • Process calculus A → B: { random i } K • Probabilistic semantics B → A: { f(i) } K A → B: “OK” if f(i) received • Asymptotic observational equivalence � “Obviously’’ authenticating protocol Q � Apply to protocols A → B: { random i } K • Protocols have specific form public channel private channel • “Attacker” is context of specific form B → A: { random j } K i , j public channel private channel A → B: “OK” if private i, j match public msgs Nondeterminism vs encryption Related work � Alice encrypts msg and sends to Bob � Canetti; B. Pfitzmann, Waidner, Backes • Interactive Turing machines A → B: { msg } K • General framework for crypto properties � Adversary uses nondeterminism • Protocol simulates an ideal setting Process E 0 c 〈 0 〉 | c 〈 0 〉 | … | c 〈 0 〉 • Universally composable security Process E 1 c 〈 1 〉 | c 〈 1 〉 | … | c 〈 1 〉 � Abadi, Rogaway, Jürjens; Process E Herzog; Warinschi c(b 1 ).c(b 2 )...c(b n ).decrypt(b 1 b 2 ...b n , msg) • Toward transfer principles between formal Dolev-Yao model and computational model In reality, at most 2-n chance to guess n-bit key Technical Challenges Syntax Expressions have size poly in |n| � Language for prob. poly - t ime functions � Bounded π -calculus with integer terms • Extend work of Cobham, Bellantoni, Cook, P :: = 0 Hofmann | c q(|n|) 〈 T 〉 send up to q(|n|) bits � Replace nondeterminism with probability • Otherwise adversary is too strong ... | c q(|n|) (x). P receive � Define probabilistic equivalence | υ c q(|n|) . P private channel • Related to poly-time statistical tests ... | [T=T] P test � Proof rules for probabilistic equivalence | P | P parallel composition • Use the proof system to derive protocol | ! q(|n|) . P bounded replication properties Terms may contain symbol n; channel width and replication bounded by poly in |n| 4
Probabilistic Semantics Scheduling � Outer term evaluation � Basic idea • Evaluate all exposed terms in parallel • Alternate between terms and processes • Multiply probabilities – Probabilistic evaluation of terms (incl. rand) � Communication – Probabilistic scheduling of parallel processes � Two evaluation phases • E(P) = set of eligible subprocesses • S(P) = set of schedulable pairs • Outer term evaluation • Prioritize – private communication first – Evaluate all exposed terms, evaluate tests • Probabilistic poly - t ime computable • Communication scheduler that makes progress – Match send and receive – Probabilistic if multiple send-receive pairs Example Complexity results � Process � Polynomial time • c 〈 rand+1 〉 | c(x).d 〈 x+1 〉 | d 〈 2 〉 | d(y). e 〈 x+1 〉 • For each closed process expression P, � Outer evaluation there is a polynomial q(x) such that – For all n • c 〈 1 〉 | c(x).d 〈 x+1 〉 | d 〈 2 〉 | d(y). e 〈 x+1 〉 Each – For all probabilistic polynomial-time prob ½ • c 〈 2 〉 | c(x).d 〈 x+1 〉 | d 〈 2 〉 | d(y). e 〈 x+1 〉 schedulers � Communication eval of P halts in time q(|n|) • c 〈 1 〉 | c(x).d 〈 x+1 〉 | d 〈 2 〉 | d(y). e 〈 x+1 〉 Choose according to probabilistic scheduler Problem: Complexity: Intuition How to define process equivalence? � Bound on number of communications � Intuition • | Prob{ C[ P ] → “yes” } - Prob{ C[ Q ] → “yes” } | < ε • Count total number of inputs, multiplying by q(|n|) to account for ! q(|n|) . P � Difficulty � Bound on term evaluation • How do we choose ε ? – Less than 1/2, 1/4, … ? (not equiv relation) • Closed T evaluated in time q T (|n|) – Vanishingly small ? As a function of what? � Bound on time for each comm step � Solution • Example: c 〈 m 〉 | c(x).P → [m/x]P • Use security parameter – Protocol is family { P n } n>0 indexed by key length • Substitution bounded by orig length of P • Asymptotic form of process equivalence – Size of number m is bounded – Previous steps preserve # occurr of x in P 5
Recommend
More recommend