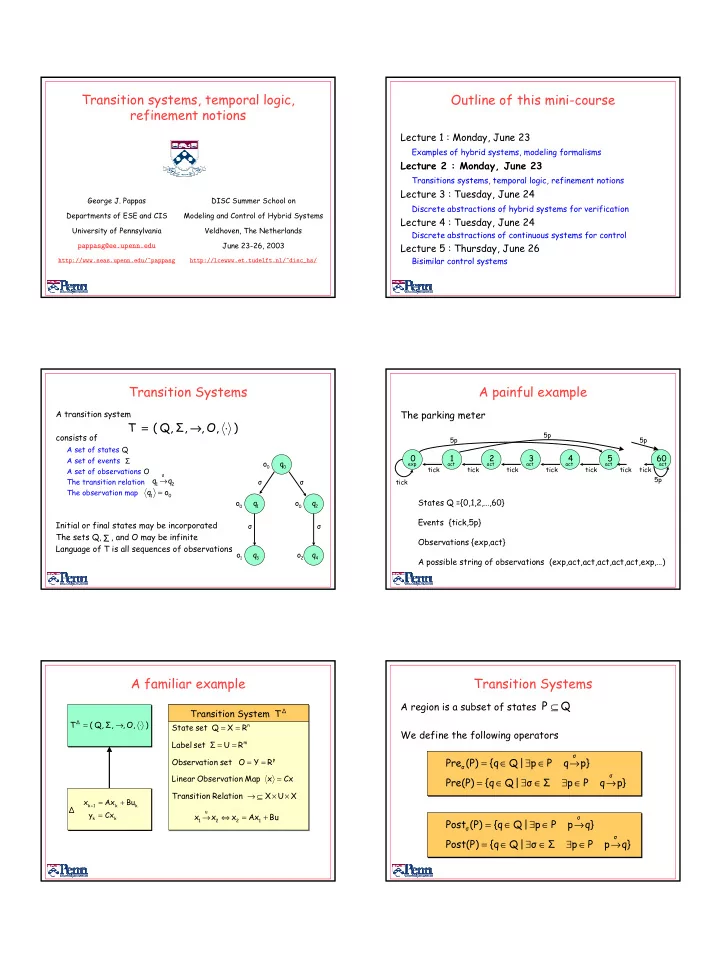

Transition systems, temporal logic, Outline of this mini-course refinement notions Lecture 1 : Monday, June 23 Examples of hybrid systems, modeling formalisms Lecture 2 : Monday, June 23 Transitions systems, temporal logic, refinement notions Lecture 3 : Tuesday, June 24 George J. Pappas DISC Summer School on Discrete abstractions of hybrid systems for verification Departments of ESE and CIS Modeling and Control of Hybrid Systems Lecture 4 : Tuesday, June 24 University of Pennsylvania Veldhoven, The Netherlands Discrete abstractions of continuous systems for control June 23-26, 2003 Lecture 5 : Thursday, June 26 pappasg@ee.upenn.edu Bisimilar control systems http://www.seas.upenn.edu/~pappasg http://lcewww.et.tudelft.nl/~disc ˙ hs/ Transition Systems A painful example A transition system The parking meter T = ( Q, Σ , → , O, ⋅ ) 5p consists of 5p 5p A set of states Q 0 1 2 3 4 5 60 A set of events Σ o q exp act act act act act act 0 0 tick tick tick tick tick tick tick A set of observations O σ q → q 5p The transition relation σ σ tick 1 2 q o The observation map = 1 0 States Q ={0,1,2,…,60} o q o q 0 1 0 2 Events {tick,5p} Initial or final states may be incorporated σ σ The sets Q, , and O may be infinite Σ Observations {exp,act} Language of T is all sequences of observations o q o q 1 3 2 4 A possible string of observations (exp,act,act,act,act,act,exp,…) A familiar example Transition Systems P ⊆ Q A region is a subset of states Transition System T ∆ T ∆ = ( Q, Σ , → , O, ⋅ ) State set Q = X = R n We define the following operators Label set Σ = U = R m σ Pre (P) {q Q | p P q p} Observatio n set O = Y = R p = ∈ ∃ ∈ → σ σ Linear Observatio n Map x Cx = Pre(P) = {q ∈ Q | ∃ σ ∈ Σ ∃ p ∈ P q → p} Transition Relation → ⊆ X × U × X T x Ax Bu = + k 1 k k + ∆ 1 u y = Cx x → x ⇔ x = Ax + Bu σ k k 1 2 2 1 Post (P) {q Q | p P p q} = ∈ ∃ ∈ → σ σ Post(P) {q Q | σ Σ p P p q} = ∈ ∃ ∈ ∃ ∈ → 1
Transition Systems Basic safety problems We can recursively define Given transition system T and regions P, S determine Forward Reachability Forward Reachability Pre (P) Pre (P) 1 = σ σ Post ã ( P ) ∩ S 6 = ∅ Pre n (P) Pre (Pre n - 1 (P)) = σ σ σ Similarly for the other operators. Also Backward Reachability Backward Reachability Pre * (P) = Pre n (P) U n ∈ N P ∩ Pre ã ( S ) 6 = ∅ Post * (P) Post n (P) = U n ∈ N Forward reachability algorithm Backward reachability algorithm Forward Forward Reachability Reachability Algorithm Algorithm Backward Backward Reachability Reachability Algorithm Algorithm R := P R := S initialize initialize while TRUE do while TRUE do R ∩ S 6 = ∅ R ∩ P 6 = ∅ if return UNSAFE ; end if; if return UNSAFE ; end if; Post ( R ) ò R Pre ( R ) ò R if return SAFE ; end if; if return SAFE ; end if; R := R ∪ Post ( R ) R := R ∪ Pre ( R ) end while end while If T is finite, then algorithm terminates (decidability). Complexity : If T is infinite, then there is no guarantee of termination. O ( n I + m R ) initial reachable states transitions Algorithmic issues More complicated problems Representation issues Enumeration for finite sets Symbolic representation for infinite (or finite) sets More sophisticated properties can be expressed using Operations on sets Linear Temporal Logic (LTL) Boolean operations Computation Tree Logic (CTL) Pre and Post computations (closure?) CTL* mu-calculus Algorithmic termination (decidability) Guaranteed for finite transition systems No guarantee for infinite transition systems 2
The basic verification problem Another verification problem Given transition system T, and temporal logic formula ϕ Given transition system T, and specification system S Basic verification problem Basic verification problem Another verification problem Another verification problem T | = ϕ L ( T ) ò L ( S ) Two main approaches Language inclusion problems Model checking : Algorithmic, restrictive Deductive methods : Semi-automated, general The basic synthesis problem Linear temporal logic (informally) Express temporal specifications along sequences Given transition system T, and temporal logic formula ϕ Informally Syntax Semantics Basic synthesis problem Basic synthesis problem Eventually p qqqqqqqqqqqqp ♦ p T k C | = ϕ Always p p pppppppppppppp If p then next q p ⇒ í q qqqqqqqqpq Synthesis in computer science assumes disturbances p until q pppppppppppppppq p U q Deep relationship between synthesis and game theory Linear temporal logic (formally) Linear temporal logic semantics Linear temporal logic syntax The LTL formulas are interpreted over infinite (omega) words w = p 0 p 1 p 2 p 3 p 4 . . . The LTL formulas are defined inductively as follows ( w, i ) | = p iff p i = p Atomic propositions All observation symbols p are formulas ( w, i ) | = ϕ 1 ∨ ϕ 2 iff ( w, i ) | = ϕ 1 or ( w, i ) | = ϕ 2 ( w, i ) | = ¬ ϕ 1 iff ( w, i ) 6 | = ϕ 1 Boolean operators If and are formulas then ϕ 1 ϕ 2 ( w, i ) | = í ϕ 1 iff ( w, i + 1) | = ϕ 1 ¬ ϕ 1 ϕ 1 ∨ ϕ 2 ( w, i ) | = ϕ 1 U ϕ 2 Temporal operators ∃ j õ i ( w, j ) | = ϕ 2 and ∀ i ô k ô j ( w, k ) | = ϕ 2 If and are formulas then ϕ 1 ϕ 2 í ϕ 1 ϕ 1 U ϕ 2 w | = þ iff ( w, 0) | = ϕ T | = þ iff ∀ w ∈ L ( T ) w | = ϕ 3
Linear temporal logic LTL examples Syntactic boolean abbreviations Two processors want to access a critical section. Each processor can has three observable states p1={inCS, outCS, reqCS} Conjunction ϕ 1 ∧ ϕ 2 = ¬ ( ¬ ϕ 1 ∨ ¬ ϕ 2 ) p2={inCS, outCS, reqCS} Implication ϕ 1 ⇒ ϕ 2 = ¬ ϕ 1 ∨ ϕ 2 Equivalence ϕ 1 ⇔ ϕ 2 = ( ϕ 1 ⇒ ϕ 2 ) ∧ ( ϕ 2 ⇒ ϕ 1 ) Mutual exclusion Both processors are not in the critical section at the same time. Syntactic temporal abbreviations ¬ ( p 1 = inCS ∧ p 2 = inCS ) Eventually ♦ ϕ = > U ϕ Always ϕ = ¬ ♦ ¬ ϕ Starvation freedom If process 1 requests entry, then it eventually enters the critical section. In 3 steps í 3 ϕ = í í í ϕ p 1 = reqCS ⇒ ♦ p 1 = inCS LTL Model Checking Computation tree logic (informally) Given transition system and LTL formula we have Express specifications in computation trees (branching time) Informally Syntax Semantics LTL model checking LTL model checking System verified Determine if T | = ϕ Inevitably next p ∀ í p p p p Counterexample LTL model checking is decidable for finite T Possibly always p ∃ p O (( n + m )( k + l )2 O ( k ) ) q p q Complexity : p formula states transitions length Comparing logics Dealing with complexity Bisimulation Simulation CTL LTL Language Inclusion CTL* 4
Language Equivalence LTL equivalence Σ T T T T Consider two transition systems and over same and O Consider two transition systems and and an LTL formula 1 2 1 2 Language equivalence Language equivalence o q o p T T 0 0 0 0 1 2 σ σ σ T 1 | = ϕ ⇔ T 2 | = ϕ If L ( T 1 ) = L ( T 2 ) then o q o q p o 0 1 0 2 1 0 σ σ σ σ Language inclusion Language inclusion o q o q o p o p 1 3 2 4 1 3 2 4 If L ( T 1 ) ò L ( T 2 ) then T 2 | = ϕ ⇒ T 1 | = ϕ Languanges are equivalent L( )=L( ) T T 1 2 Language equivalence and inclusion are difficult to check Simulation Relations Game theoretic semantics Consider two transition systems Simulation is a matching game between the systems T = ( Q , Σ , → , O, ⋅ ) 1 1 1 1 o q o p T T T = ( Q , Σ , → , O, ⋅ ) 0 0 0 0 1 2 2 2 2 2 σ σ σ S Q Q ⊆ × over the same set of labels and observations. A relation 1 2 o q o q o p is called a simulation relation if it 0 1 0 2 1 0 1. Respects observations σ σ σ σ if (q, p) ∈ S then q = p 1 2 o q o q o p o p 1 3 2 4 1 3 2 4 2. Respects transitions σ σ if (q, p) ∈ S and q → q' , then p → p' for some (q' , p' ) ∈ S T ≤ T T ≤ T Check that but it is not true that 1 2 2 1 T ≤ T If a simulation relation exists, then 1 2 The parking example Simulation relations The parking meter Consider two transition systems and T T 1 2 5p Simulation implies language inclusion Simulation implies language inclusion 5p 5p If T 1 ô T 2 then L ( T 1 ) ò L ( T 2 ) 0 1 2 3 4 5 60 exp act act act act act act tick tick tick tick tick tick tick 5p tick A coarser model 5p Complexity of tick L ( T 1 ) ò L ( T 2 ) O (( n 1 + m 1 )2 n 2 ) 0 many exp act tick 5p tick Complexity of T 1 ô T 2 O (( n 1 + m 1 )( n 2 + m 2 )) S = {(0,0), (1, many),..., (60, many)} 5
Recommend
More recommend