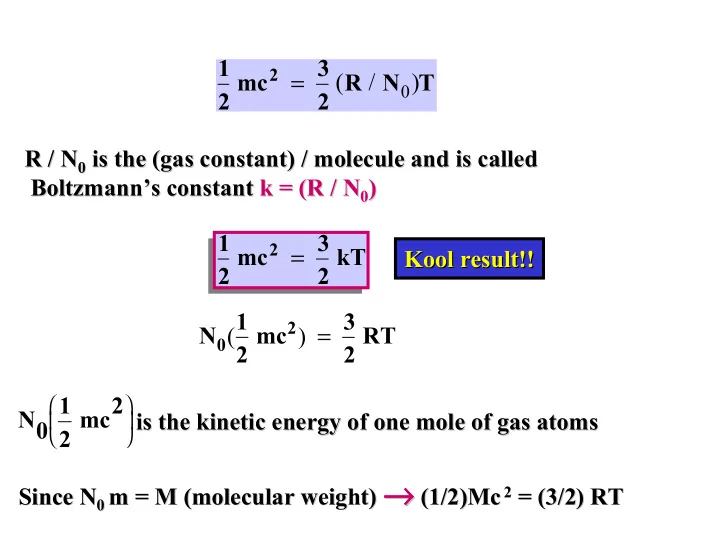

1 2 mc 2 = 3 ( R / N 0 ) T 2 R / N 0 is the (gas constant) / molecule and is called R / N 0 is the (gas constant) / molecule and is called Boltzmann’s constant constant k = (R / N k = (R / N 0 ) Boltzmann’s 0 ) 1 2 mc 2 = 3 2 kT Kool result!! result!! Kool N 0 ( 1 2 mc 2 ) = 3 2 RT 1 2 mc2 N0 is the kinetic energy of one mole of gas atoms is the kinetic energy of one mole of gas atoms → → → → (1/2) m = M (molecular weight) → → 2 = (3/2) RT → → Since N 0 (1/2)Mc Mc 2 = (3/2) RT Since N 0 m = M (molecular weight)
Units: Units: mc 2 is a kinetic energy, therefore is a kinetic energy, therefore 2 mc 2 PV = n 2 N 0 must also have units of energy must also have units of energy 3 2 PV ~ [pressure] [volume] [volume] PV ~ [pressure] = [(force / Area)] [(Area) (Length)] [(Area) (Length)] = [(force / Area)] × × length PV ~ force × × × × length PV ~ force × × Energy = Force × × × × × Distance × Distance Energy = Force × ×
Bonus * Bonus * Bonus * Bonus * Bonus * Bonus Bonus * Bonus * Bonus * Bonus * Bonus * Bonus
Bonus * Bonus * Bonus * Bonus * Bonus * Bonus Bonus * Bonus * Bonus * Bonus * Bonus * Bonus
Typical Molecular Speeds Typical Molecular Speeds c 2 = c rms [Root Mean Square Speed] [Root Mean Square Speed] Understand that c = Understand that [Later we will define c c rms more fully.] [Later we will define rms more fully.] → → → → c = (3kT/m) 1/2 1/2 → → c = (3kT/m) → → (1/2)mc 2 2 = (3/2) = (3/2)kT kT (1/2)mc Notice: c = (3N 0 kT/N 0 m) 1/2 1/2 [N 0 is Avagadro’s Avagadro’s number] number] Notice: c = (3N 0 kT/N 0 m) [N 0 is But N 0 k = R and N 0 m = M (molecular weight) But N 0 k = R and N 0 m = M (molecular weight) 2 = 3RT/M c = (3RT/M) 1/2 1/2 → → → → c 2 = 3RT/M c = (3RT/M) → → → → c Consider Gas with At wt of 0.001 Kg/mole (H atoms!) Consider Gas with At wt of 0.001 Kg/mole (H atoms!) R= 8.314 Joules/mole- -deg deg, T = 300 , T = 300 deg deg R= 8.314 Joules/mole 2 = 6 Joules/Kg = 7.47 6 (m/sec) c 2 = 3RT/M 3RT/M = 7.47 = 7.47 × × × 10 × × × 10 6 Joules/Kg = 7.47 × × 10 × × × × 10 6 (m/sec) 2 c × × × × 2
Typical Molecular Speeds Typical Molecular Speeds c 2 = c rms Understand that c = [Root Mean Square Speed] [Root Mean Square Speed] Understand that → → → → → → → → (1/2)mc 2 2 = (3/2) = (3/2)kT kT (1/2)mc c = (3kT/m) 1/2 1/2 c = (3kT/m) Consider Gas with At wt of 0.001 Kg/mole (H atoms!) Consider Gas with At wt of 0.001 Kg/mole (H atoms!) 23 molecule / mole) × 10 × × × m = (0.001 Kg / mole) / (6.02 × × × × 10 23 molecule / mole) m = (0.001 Kg / mole) / (6.02 27 Kg/molecule = 1.66 × × 10 × × × × 10 - Kg/molecule = 1.66 × × -27 23 Joules/molecule k = 1.38 × × × 10 × × × 10 - Joules/molecule - - deg deg, , T = 300 deg deg k = 1.38 × × -23 T = 300 2 = 6 Joules/Kg = 7.47 6 (m/sec) c 2 = 3kT/m 3kT/m = 7.47 = 7.47 × × × × × 10 × 10 6 Joules/Kg = 7.47 × × × 10 × × × 10 6 (m/sec) 2 c × × × × 2
3 m/sec × × × × 10 c = 2.73 × × × × 10 3 m/sec (Fast Moving Particle) c = 2.73 (Fast Moving Particle) 3 m/sec for He = 0.004 Kg/mole c = 1.37 × × × × × 10 × 10 3 m/sec for He = 0.004 Kg/mole c = 1.37 × × c 1200 = 2 c 300 , → → → → c 1200 = 2 c 300 , 1/2 → → → → Note c ~ T 1/2 Note c ~ T c H 2 = 4c O 2 ( M H 2 = 2 , M O 2 = 32 ) → → → → 1/2 → → → → Note c ~ 1/m 1/2 Note c ~ 1/m Why do Light and Heavy Gases Exert Same Pressure at Why do Light and Heavy Gases Exert Same Pressure at Constant V,T, n (# moles)? (p = nRT nRT/V) /V) Constant V,T, n (# moles)? (p = wall collision frequency/unit area = wall collision frequency/unit area = However, since However, since (1/6) (N/V) (Ac t)/(At) = (1/6) (N/V) c (1/6) (N/V) (Ac t)/(At) = (1/6) (N/V) c 1 Lighter molecules collide with wall more Lighter molecules collide with wall more c ~ c ~ m frequently than heavy molecules! frequently than heavy molecules!
BUT momentum change momentum change per collision ~ per collision ~ mc mc, with , with BUT m m mc ~ ~ ~ ~ mc m Thus, heavier molecules transfer more momentum Thus, heavier molecules transfer more momentum per impact per impact Two effects cancel since (1/m 1/2 1/2 ) x (m ) x (m 1/2 1/2 ) is independent of m ) is independent of m Two effects cancel since (1/m Result is that p scales like n, the number of moles or Result is that p scales like n, the number of moles or the number of particles! pV pV = = nRT nRT the number of particles!
Experimental Evidence for Kinetic Theory: Effusion Experimental Evidence for Kinetic Theory: Effusion Put very small hole in box and measure # of molecules Put very small hole in box and measure # of molecules coming through. If hole is really small , molecules won’t coming through. If hole is really small , molecules won’t know it’s there and will collide with hole at same rate as know it’s there and will collide with hole at same rate as they collide with the wall. they collide with the wall.
Effusion Effusion of Gases: of Gases: The Movie The Movie Note: Note: ← ← ← ← ← ← ← ← Hole Hole QuickTime™ and a Video decompressor are needed to see this picture. Must be Must be very small! very small!
Effusion of a Gas through a Small Hole Effusion of a Gas through a Small Hole Vacuum Gas Vacuum Gas
If hole area = A, rate at which molecules If hole area = A, rate at which molecules leave = (1/6) (N / V) Ac = R leave = (1/6) (N / V) Ac = R For two different molecular speeds c 1 , c 2 and For two different molecular speeds c 1 , c 2 and concentrations N 1 /V, N 2 /V: concentrations N 1 /V, N 2 /V: R 1 N 1 / N 2 c 1 = R 2 V V c 2 If N 1 = N 2 (equal initial concentrations) If N 1 = N 2 (equal initial concentrations) 3kT m 1 R 1 = c 1 (R 1 /R 2 )=(m 2 /m 1 ) 1/2 1/2 (R 1 /R 2 )=(m 2 /m 1 ) = → → → → → → → → 3kT R 2 c 2 m 2
R 1 32 = 2 = 4 → → → → 2 → → → → For m 1 being H 2 and m 2 being O 2 For m 1 being H 2 and m 2 being O R 2 Find experimentally that light gases escape more Find experimentally that light gases escape more quickly than heavy ones! quickly than heavy ones! Experimental Evidence for Kinetic Theory:Heat Capacities Experimental Evidence for Kinetic Theory:Heat Capacities Definition: Heat in calories needed to raise temperature Definition: Heat in calories needed to raise temperature ° centigrade. ° of 1 mole of a substance 1 ° ° ° ° ° ° centigrade. of 1 mole of a substance 1 Two kinds: C Two kinds: C p p (add heat at constant pressure) (add heat at constant pressure) C v (add heat at constant volume) C v (add heat at constant volume) Adding heat means adding energy. Energy goes two places: Adding heat means adding energy. Energy goes two places:
(1) Increases kinetic energy of molecules: (1) Increases kinetic energy of molecules: KE = (1/2) mc 2 , c 2 ~ T KE = (1/2) mc 2 , c 2 ~ T (2) Perform work. (2) Perform work. As we shall see shortly, no work is done As we shall see shortly, no work is done at constant volume. at constant volume. C v : volume constant. All heat goes to KE. Compute as follows: C v : volume constant. All heat goes to KE. Compute as follows: KE [1 mole gas] = 1 2 mc 2 × N 0 = 3 2 kTN 0 = 3 2 RT KE [1 mole gas] = Increase T from T 1 to T 2 : KE 1 =(3/2)RT 1 & KE 2 =(3/2)RT 2 Increase T from T 1 to T 2 : KE 1 =(3/2)RT 1 & KE 2 =(3/2)RT 2 KE 2 − KE 1 = 3 1 ) = energy to increase T form T 2 R ( T 2 − T energy to increase T form T 1 to T 2 1 to T 2 By definition when T 2 -T T 1 = 1 ° ° ° ° ° ° ° ° KE 2 - KE KE 1 = C C v By definition when T 2 - 1 = 1 KE 2 - 1 = v C v = (3/2) R C v = (3/2) R (Independent of T for an ideal gas) (Independent of T for an ideal gas) ≅ ≅ ≅ ≅ 3 cal / mole (C C v v ≅ ≅ ≅ ≅ 3 cal / mole - - deg deg) ) (
C p : Pressure constant so volume increases with increase C p : Pressure constant so volume increases with increase in T. As we see below, work is done in this case: in T. As we see below, work is done in this case: L A L p = F / A A Gas ← Movable Piston ← Gas ← ← ← ← ← ← Movable Piston T 1 T T 2 T 1 2 work = F F × × L = ( × × × × L = (Ap Ap) ) × × × × × L = p x (AL) × L = p x (AL) work = × × × × But, AL = V 2 - V V 1 = ∆ ∆ ∆ V (volume change) ∆ ∆ ∆ V (volume change) But, AL = V 2 - 1 = ∆ ∆ ∆ T ∆ work = p x (AL) p x (AL) = p(V = p(V 2 - V V 1 ) = nR nR(T (T 2 -T T 1 ) = nR nR ∆ ∆ ∆ ∆ T work = 2 - 1 ) = 2 - 1 ) = ∆ ∆ → → → → → → → → ∆ T=1 ∆ ∆ ∆ ° ° ° ° , w = R For n=1 mole, ∆ ∆ ∆ ∆ T=1 ° ° ° ° , w = R For n=1 mole, w = p ∆ V = nR nR ∆ ∆ ∆ T ∆ ∆ ∆ T w = p ∆ V = ∆ ∆ To raise temperature of one mole of gas by one degree To raise temperature of one mole of gas by one degree must do R units of work. must do R units of work.
Recommend
More recommend